JAVA 자료구조 2(Data Structure)
Step 4 : 비선형구조
트리(Tree)
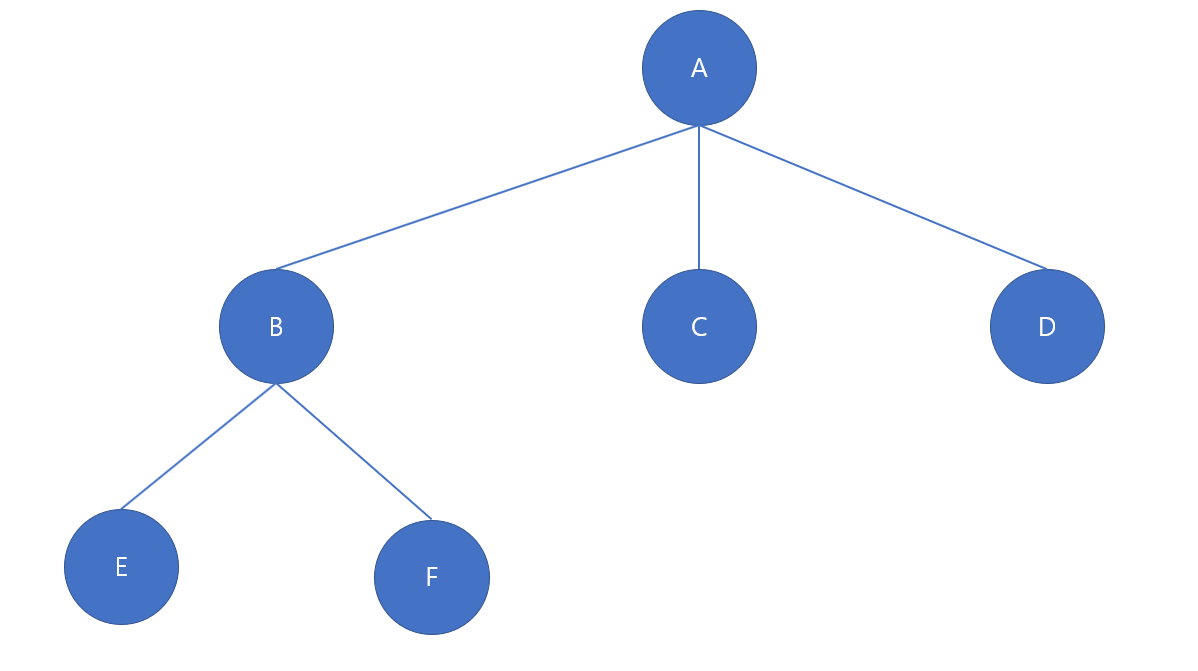트리란 위에도 가볍게 언급한, 하나의 루트 노드와 0개 이상의 자식노드로 이루어진 자료구조입니다. 주로 계층적 관계( Hierarchical Relationship )를 표현하는 자료구조입니다. 트리관련 용어를 살펴보겠습니다.
- Node (노드): A,B,C와 같은 요소입니다.
- Root Node (루트노드): 최상위 노드 즉 A노드입니다.
- Edge (간선) : 노드와 노드를 연결한 선입니다.
- Terminal node, Leaf Node (단말노드) : 자식 노드가 없는 E, F, C, D와 같은 노드입니다.
- Internal Node(내부노드) : 단말 노드가 아닌 A, B와 같은 노드입니다.
- Degree(차수) : 자식 노드의 수를 말합니다.
- Preorder Traversal( 전위 순회 ) : Root -> 좌 -> 우 순으로 Tree를 탐색하는 방법입니다.
- Inorder Traversal( 중위 순회 ) : 좌 -> root -> 우 순으로 Tree를 탐색하는 방법입니다.
- Postorder Traversal ( 후위 순회 ) : 좌 -> 우 -> root순으로 tree를 탐색합니다.
Tree의 자료구조를 표현하는 방법은 배열과 LinkedList로 표현할 수 있습니다.
이진 트리( Binary Tree )
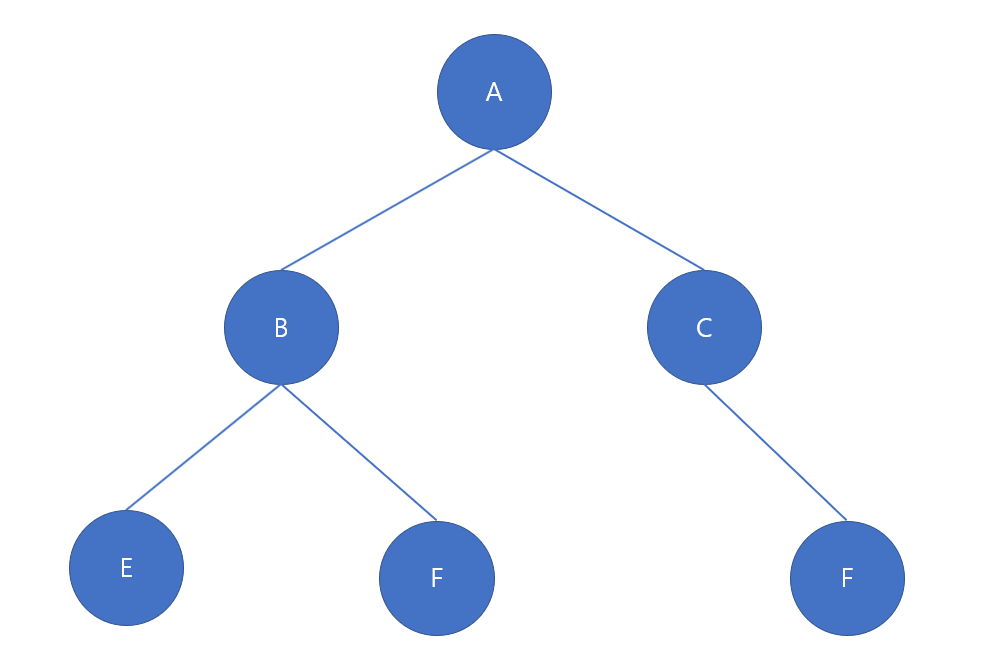각 노드가 최대 두 개의 자식을 갖는 Tree입니다. 꼭 자식 노드가 다 차지 않아도 됩니다.
완전 이진 트리 ( Complete Binary Tree )
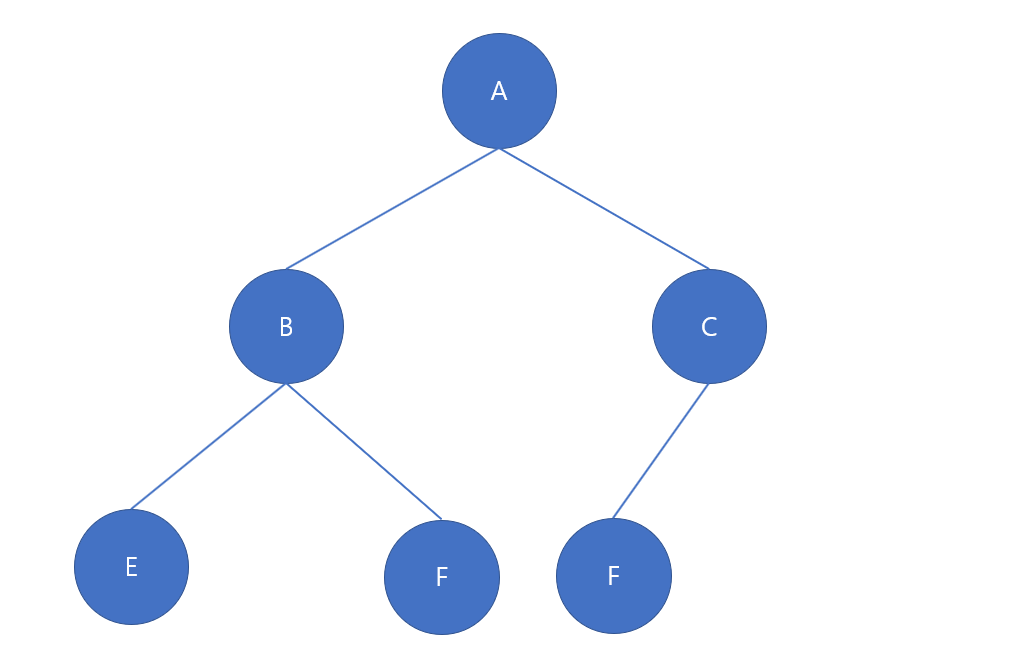마지막 레벨을 제외한 모든 노드는 채워져 있어야 하며 마지막 레벨은 왼쪽부터 채워져 있는 Binary Tree를 말합니다.
정 이진트리 ( Full Binary Tree )
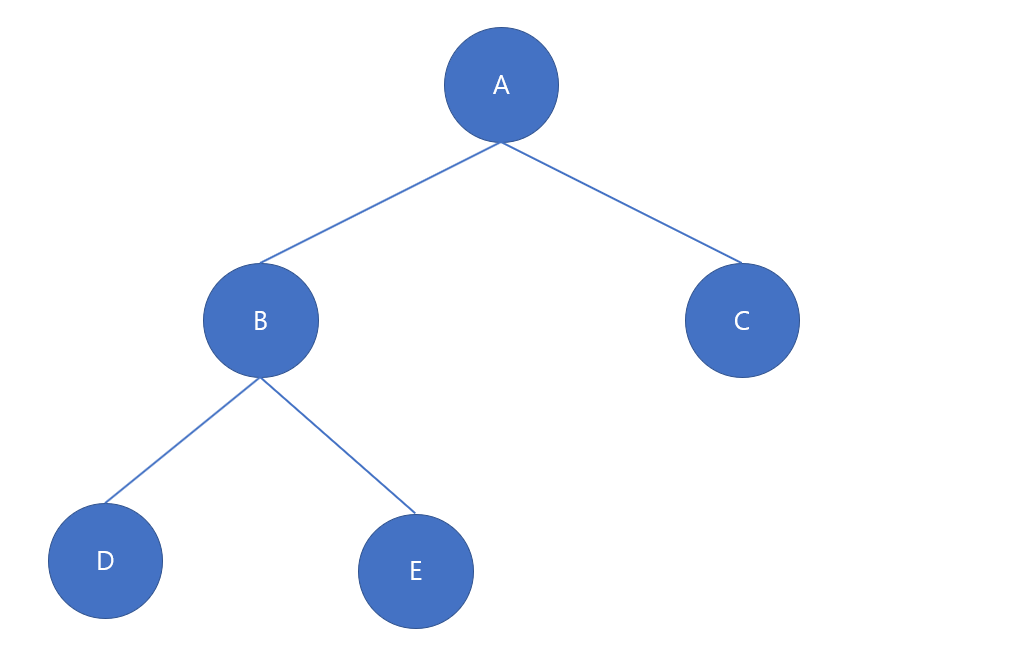모든 노드가 0개 또는 2개의 자식 노드를 갖는 이진트리입니다.
포화 이진트리 ( Perfect Binary Tree )
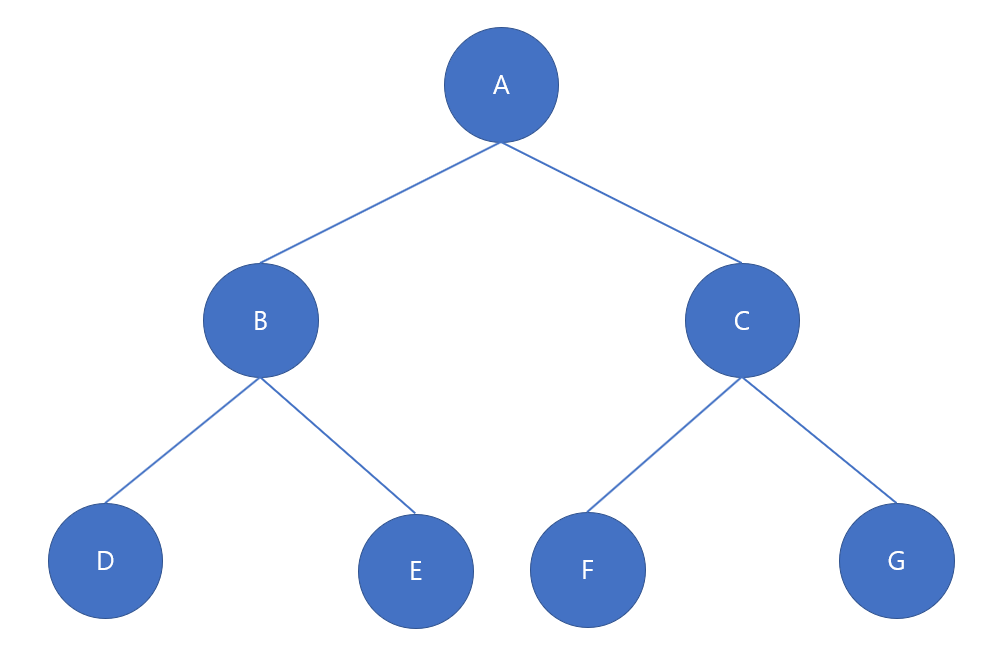모든 레벨의 노드가 꽉 차있는 이진트리입니다.
이진 탐색 트리 ( Binary Search Tree )
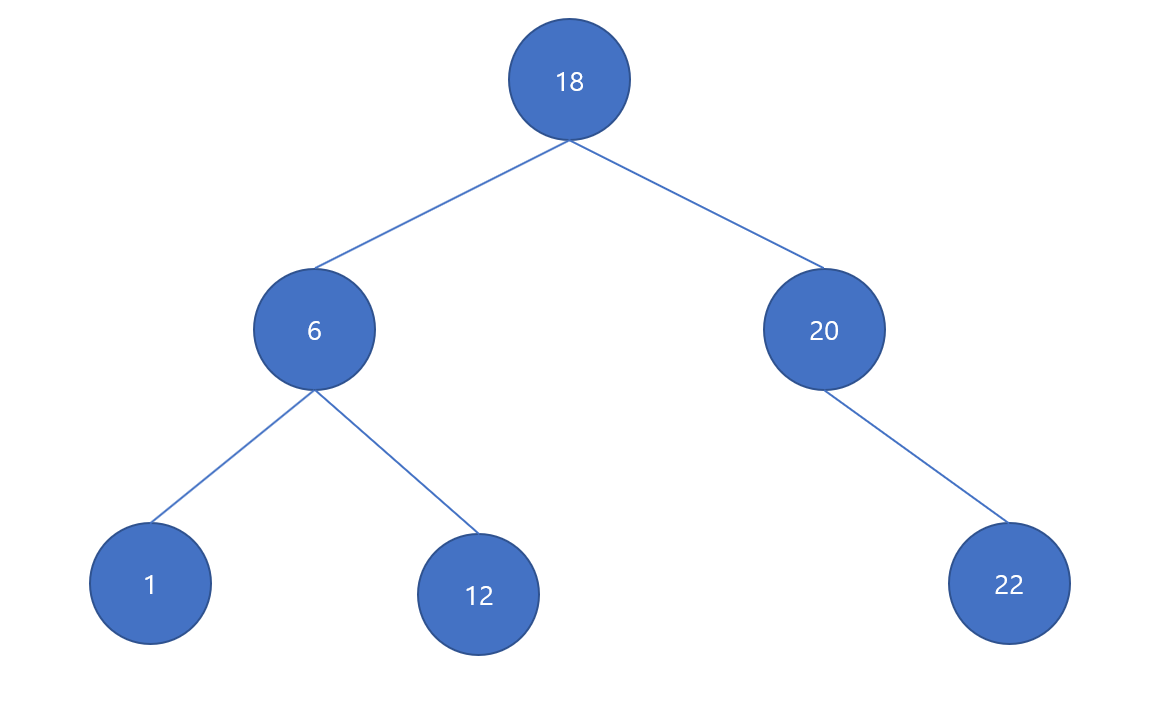
중복된 값이 없으면서 왼쪽 자식 노드 값 < root 노드 < 오른쪽 자식 노드 값을 만족하는 이진트리입니다. root 노드 하위 왼쪽 노드 집합들은 root 노드 값보다 작아야 하며 우측 집합은 커야 합니다.
Tree구조로 할 수 있는 것은 다양합니다. 언급하지는 않았지만, Expression Tree와 같은 형태로 들어온 데이터를 구성할 수도 있고 새로운 형식의 데이터를 만들어 담을 수도 있습니다. 이제 Tree를 어떻게 구성하는지 알아보겠습니다.
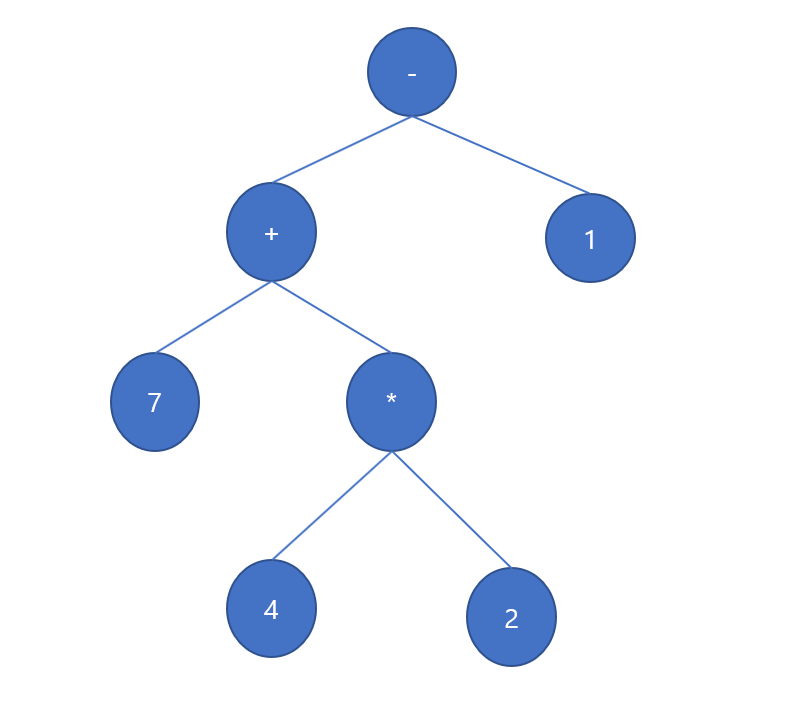
ex) 수식 트리 Expression Tree
수식을 tree형태로 분리한 tree
7 + 4 * 2 -1 를 나타낸 트리는 아래와 같습니다.
Linked List로 Tree 구현
트리는 원하는 방식으로 원하는 모양으로 무궁무진하게 만들 수 있습니다. 단순한 이진 트리를 구현해보겠습니다.
- getValue() : 노드에 저장된 데이터 return
- setLeftNode() : 왼쪽 노드 세팅
- setRightNode() : 우측 노드 세팅
- getLetNode(): 좌측 노드 데이터 return
- getRightNode(): 우측 노드 데이터 return
- inOrderTraversal() : 중위 순회 왼쪽 node -> root node -> 오른쪽 node
- preOrderTraversal() : root node -> 왼쪽 node -> 오른쪽 node
- postOrderTraversal() : 왼쪽 node -> 오른쪽 node -> root node
public class TreeWithLinkedList<T> {
private T value;
private TreeWithLinkedList<T> leftNode;
private TreeWithLinkedList<T> rightNode;
public TreeWithLinkedList( T value ) {
this.value = value;
}
/**
* left -> root -> right
*/
public void inOrderTraversal() {
if( leftNode != null ) leftNode.inOrderTraversal();
System.out.println(value.toString());
if( rightNode != null ) rightNode.inOrderTraversal();
}
/**
* root -> left -> right
*/
public void preOrderTraversal() {
System.out.println(value.toString());
if( leftNode != null ) leftNode.preOrderTraversal();
if( rightNode != null ) rightNode.preOrderTraversal();
}
/**
* left -> right -> root
*/
public void postOrderTraversal() {
if( leftNode != null ) leftNode.postOrderTraversal();
if( rightNode != null ) rightNode.postOrderTraversal();
System.out.println(value.toString());
}
public T getValue() {
return value;
}
public void setValue(T value) {
this.value = value;
}
public TreeWithLinkedList<T> getLeftNode() {
return leftNode;
}
public void setLeftNode(TreeWithLinkedList<T> leftNode) {
this.leftNode = leftNode;
}
public TreeWithLinkedList<T> getRightNode() {
return rightNode;
}
public void setRightNode(TreeWithLinkedList<T> rightNode) {
this.rightNode = rightNode;
}
}
TreeWithLinkedList<Integer> root = new TreeWithLinkedList<Integer>(1);
TreeWithLinkedList<Integer> rootLeft = new TreeWithLinkedList<Integer>(2);
TreeWithLinkedList<Integer> rootRight = new TreeWithLinkedList<Integer>(3);
TreeWithLinkedList<Integer> rootLeftLeft = new TreeWithLinkedList<Integer>(4);
TreeWithLinkedList<Integer> rootLeftRight = new TreeWithLinkedList<Integer>(5);
root.setLeftNode(rootLeft);
root.setRightNode(rootRight);
rootLeft.setLeftNode(rootLeftLeft);
rootLeft.setRightNode(rootLeftRight);
root.inOrderTraversal(); // 중위순회 left -> root -> right >> 4 2 5 1 3
root.preOrderTraversal(); // 전위순회 root -> left -> right >> 1 2 4 5 3
root.postOrderTraversal(); // 후위순회 left -> right -> root >> 4 5 2 3 1
배열로 Tree 구현
배열로 2진트리를 구성하려면 우선 배열의 크기를 정해야 하기 때문에 최종 데이터의 크기를 알아야 한다는 점, 왼쪽 노트의 위치, 우측 노드의 위치, 부모 위치 구하는 방법을 알아야합니다.
- 왼쪽 자식의 index : ( 자기자신의 index ) * 2 +1
- 오른쪽 자식의 index : 왼쪽 자식의 index + 1 = ( 자기자신의 index ) * 2 +2
- 부모 index : ( 자기 자신의 index -1 ) / 2
- 총 크기 : Perfect Binary Tree 크기 만큼 하기 위해, 최종 데이터의 크기를 꽉 찬 트리 size로 만든후 그 크기 * 2 배만큼의 크기가 필요합니다.
public class TreeWithArray<T> {
private Object tree [];
private int treeSize;
public TreeWithArray( int arraySize ) {
treeSize = 1;
while (treeSize < arraySize) {
treeSize <<= 1;
}
treeSize *= 2;
tree = new Object[ treeSize ];
}
/**
* left -> root -> right
*/
public void inOrderTraversal( int checkIndex ) {
if( checkIndex < treeSize && tree[checkIndex] != null ) {
int leftChildIndex = getLeftNodeIndex(checkIndex);
int rightChildIndex = getRightNodeIndex(checkIndex);
inOrderTraversal( leftChildIndex );
System.out.println(tree[checkIndex].toString());
inOrderTraversal( rightChildIndex );
}
}
/**
* root -> left -> right
*/
public void preOrderTraversal( int checkIndex ) {
if( checkIndex < treeSize && tree[checkIndex] != null ) {
int leftChildIndex = getLeftNodeIndex(checkIndex);
int rightChildIndex = getRightNodeIndex(checkIndex);
System.out.println(tree[checkIndex].toString());
preOrderTraversal( leftChildIndex );
preOrderTraversal( rightChildIndex );
}
}
/**
* left -> right -> root
*/
public void postOrderTraversal( int checkIndex ) {
if( checkIndex < treeSize && tree[checkIndex] != null ) {
int leftChildIndex = getLeftNodeIndex(checkIndex);
int rightChildIndex = getRightNodeIndex(checkIndex);
postOrderTraversal( leftChildIndex );
postOrderTraversal( rightChildIndex );
System.out.println(tree[checkIndex].toString());
}
}
@SuppressWarnings("unchecked")
public T getValue( int index ) {
return (T)tree[index];
}
public void setValue( T value, int index ) {
if( index >= treeSize ) {
throw new IndexOutOfBoundsException("size를 확인하세요");
}
tree[index] = value;
}
@SuppressWarnings("unchecked")
public T getLeftNode( int parentIndex ) {
int childIndex = getLeftNodeIndex(parentIndex);
if( childIndex >= treeSize ) {
throw new IndexOutOfBoundsException("size를 확인하세요");
}
return (T)tree[childIndex];
}
public void setLeftNode( T leftNode, int parentIndex ) {
int childIndex = getLeftNodeIndex( parentIndex );
if( childIndex >= treeSize ) {
throw new IndexOutOfBoundsException("size를 확인하세요");
}
tree[childIndex] = leftNode;
}
@SuppressWarnings("unchecked")
public T getRightNode( int parentIndex ) {
int childIndex = getRightNodeIndex( parentIndex );
if( childIndex >= treeSize ) {
throw new IndexOutOfBoundsException("size를 확인하세요");
}
return (T)tree[childIndex];
}
public void setRightNode( T rightNode, int parentIndex) {
int childIndex = getRightNodeIndex( parentIndex );
if( childIndex >= treeSize ) {
throw new IndexOutOfBoundsException("size를 확인하세요");
}
tree[childIndex] = rightNode;
}
public int getLeftNodeIndex( int parentIndex ) {
return parentIndex*2 +1;
}
public int getRightNodeIndex( int parentIndex ) {
return parentIndex*2 +2;
}
}
TreeWithArray<Integer> tree = new TreeWithArray<Integer>(5);
tree.setValue(1, 1);
tree.setLeftNode(2, 1);
tree.setRightNode(3, 1);
tree.setLeftNode(4, tree.getLeftNodeIndex(1));
tree.setRightNode(5, tree.getLeftNodeIndex(1));
tree.inOrderTraversal(1); // 중위순회 left -> root -> right >> 4 2 5 1 3
tree.preOrderTraversal(1); // 전위순회 root -> left -> right >> 1 2 4 5 3
tree.postOrderTraversal(1); // 후위순회 left -> right -> root >> 4 5 2 3 1
그래프
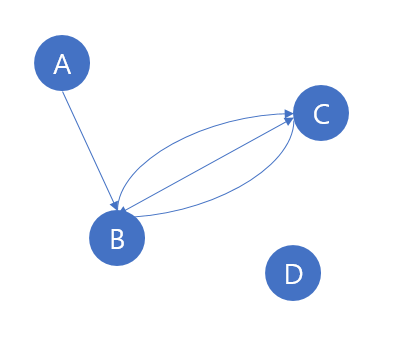
그래프란 위 그림에서 보는 것처럼 노드와 노드를 연결한 간선이 존재하는 자료구조입니다. 이전 자료구조를 공부하면서 봤었던 용어들입니다.
- Vertex (정점) : 하나의 노드를 말합니다.
- Edge (간선) : 정점을 연결하는 선입니다.
- Adjacent vertex ( 인접정점 ) : 자기 자신 정점과 바로 연결된 정점을 말합니다.
- Degree ( 차수 ) : 자기 자신과 연결된 간선의 개수를 말합니다.
- Cycle : 한 정점에서 시작하여 자기자신으로 끝나는 경로를 말합니다.
- 오일러 경로 : 그래프에 존재하는 모든 간선을 한 번만 통과하는 것 » 오일러 경로는 차수가 홀수인 정점이 2개일때 존재합니다.
- 오일러 회로 : 오일러 경로 + 시작점과 끝점이 같은 경우 = 한 붓 그리기 » 차수가 홀수인 정점이 0개일때 오일러 회로가 존재합니다.
방향 그래프
그래프에 방향이 존재하여 G(A,B)는 G(B,A)는 다른 경우를 말합니다.
무방향 그래프
그래프에 방향이 존재하지 않아 양 방향으로 갈 수 있다. G(A,B)는 G(B,A)와 동일한 경우를 말합니다.
가중치 그래프(Weighted Graph)
간선에 비용이나 가중치가 할당된 그래프를 말합니다.
솔직히 업무에서 그래프를 다루거나 사용한 사례는 없어 잘 아는 자료구조는 아닙니다. 단지 백준 알고리즘 혹은 카카오 알고리즘을 풀어 볼 때 관련 내용 등장하면 사용 및 공부하기 위해 정리합니다. 그래프 자료구조를 구현하는 방법은 크게 두 가지가 존재합니다. 하나는 인접 리스트로 구현하는 방법과, 인접행렬로 구현하는 방법입니다.
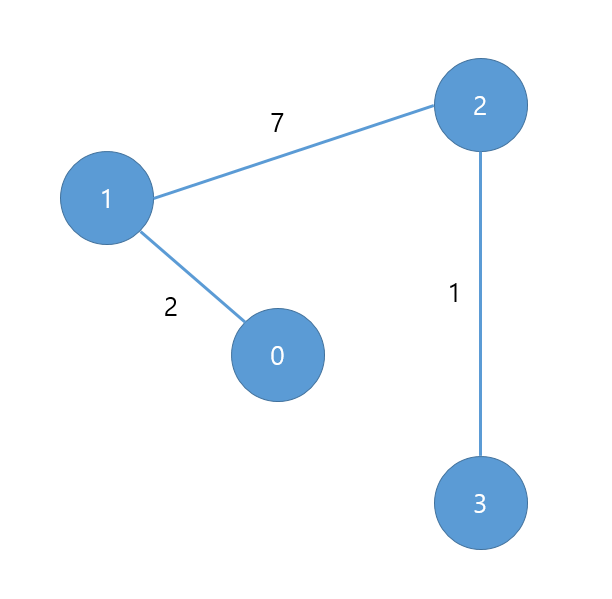
인접 리스트(Adjacency List)로 구현
내용은 간단합니다. 배열의 index는 자기 자신의 노드 위치를 말하며, 저장된 value는 해당 노드와 연결된 인접 노드를 가리킵니다. 추가로 두 노드 사이의 가중치를 저장하도록 양방향 그래프로 구현해보겠습니다.
- push() : 데이터 삽입.
public class GraphArrayList {
private ArrayList<ArrayList<int[]>> graph;
// 정점의 개수로 초기화
public GraphArrayList( int nodeSize ) {
this.graph = new ArrayList<ArrayList<int[]>>();
// 각각의 정점들 초기화
for( int index=0; index < nodeSize; index++ ) {
graph.add( new ArrayList<int[]>() );
}
}
public void push( int orignalNode, int adjacentNode, int weight ) {
pushOnly( orignalNode, adjacentNode, weight );
pushOnly( adjacentNode, orignalNode, weight );
}
private void pushOnly( int orignalNode, int adjacentNode, int weight ) {
int[] temp = { adjacentNode, weight };
graph.get(orignalNode).add(temp);
}
public void print() {
for (int index = 0; index < graph.size(); index++) {
System.out.println("정점 " + index + "의 인접리스트");
for (int indexInner = 0; indexInner < graph.get(index).size(); indexInner++) {
int[] temp = graph.get(index).get(indexInner);
System.out.print( temp[0]+"("+temp[1]+")" + " ");
}
System.out.println();
}
}
}
GraphArrayList graph = new GraphArrayList(4);
graph.push(0, 1, 2);
graph.push(1, 2, 7);
graph.push(2, 3, 1);
graph.print();
1
2
3
4
5
6
7
8
9
// 출력
정점 0의 인접리스트
1(2)
정점 1의 인접리스트
0(2) 2(7)
정점 2의 인접리스트
1(7) 3(1)
정점 3의 인접리스트
2(1)
인접 행렬(Adjacency Matrix)로 구현
구현 내용은 간단합니다. 2차원 배열에 index가 두 노드의 연결 여부 및 가중치를 나타냅니다. 아래 코드를 보면 이해가 될 것입니다.
public class GraphMatrix {
private int[][] graph;
public GraphMatrix( int nodeSize ) {
graph = new int [nodeSize][nodeSize];
}
public void push( int orignalNode, int adjacentNode, int weight ) {
graph[orignalNode][adjacentNode] = weight;
graph[adjacentNode][orignalNode] = weight;
}
public void print() {
for (int index = 0; index < graph.length; index++) {
System.out.println("정점 " + index + "의 인접리스트");
for (int indexInner = 0; indexInner < graph[index].length; indexInner++) {
if( graph[index][indexInner] > 0) {
System.out.print( indexInner+"("+graph[index][indexInner]+")" + " ");
}
}
System.out.println();
}
}
}
GraphMatrix graph = new GraphMatrix(4);
graph.push(0, 1, 2);
graph.push(1, 2, 7);
graph.push(2, 3, 1);
graph.print();
1
2
3
4
5
6
7
8
9
//출력
정점 0의 인접리스트
1(2)
정점 1의 인접리스트
0(2) 2(7)
정점 2의 인접리스트
1(7) 3(1)
정점 3의 인접리스트
2(1)
이런 그래프를 일반적으로 탐색하는 방법은 2가지입니다. 하나는 깊이우선탐색(DFS), 다른 하나는 너비 우선 탐색(BFS)입니다.
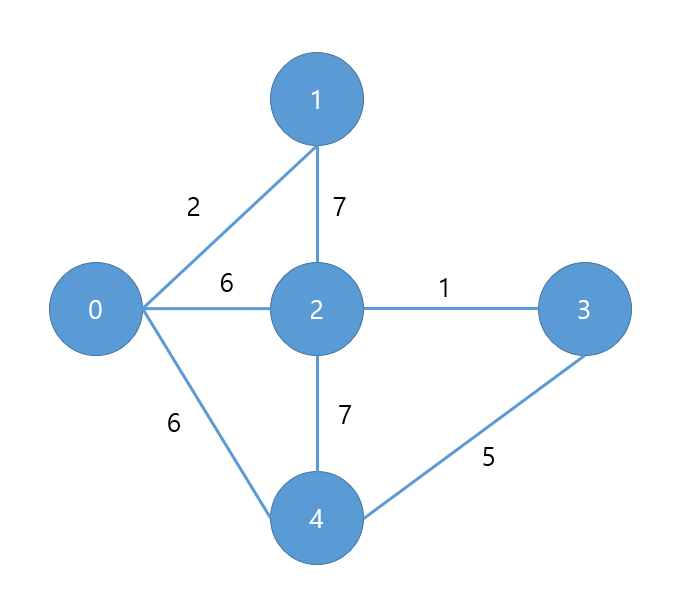
깊이우선탐색( Depth First Search )
하나의 정점에서 시작하여 다음 인접 노드를 지속해서 확인하여 모든 노드를 탐색하는 방법입니다. 원리는 root노드를 정한 후 인접 노드를 stack에 집어넣고 stack을 순회하면서 호출된 적 있는지 확인 후 반복하는 일만 진행하면 됩니다.
너비우선탐색 ( Breadth First Search )
하나의 정점에서 시작하여 하나의 정점을 완벽히 탐색 후 다음 정점을 넘어가 모든 노드를 탐색하는 방법입니다. 원리는 간단합니다. root노드를 정한 후 root노드에 관련된 인접 노드를 que에 집어넣고 해당 que를 순회하면서 한 번 호출된 적 있는 노드인지 확인 후 que가 빌 때까지 지속하는 방법입니다.
public class GraphMatrix {
private int[][] graph;
private int nodeSize = 0;
public GraphMatrix( int nodeSize ) {
graph = new int [nodeSize][nodeSize];
this.nodeSize = nodeSize;
}
public void push( int orignalNode, int adjacentNode, int weight ) {
graph[orignalNode][adjacentNode] = weight;
graph[adjacentNode][orignalNode] = weight;
}
public void bfs() {
if( nodeSize == 0 ) {
throw new IndexOutOfBoundsException(" 노드가 비어있습니다.");
}
int[] cache = new int[nodeSize];
Queue<Integer> nodesQue = new LinkedList<>();
bfsLoopChecking(0, cache, nodesQue);
}
public void dfs() {
if( nodeSize == 0 ) {
throw new IndexOutOfBoundsException(" 노드가 비어있습니다.");
}
int[] cache = new int[nodeSize];
Stack<Integer> nodesStack = new Stack<Integer>();
dfsLoopChecking(0, cache, nodesStack);
}
private void bfsLoopChecking( int orignalNode, int[] cache , Queue<Integer> nodesQue ) {
nodesQue.add( orignalNode );
while ( !nodesQue.isEmpty() ) {
Integer nextNodes = nodesQue.poll();
if( cache[nextNodes] == 0 ){
cache[nextNodes] = 1;
System.out.println( nextNodes + " 탐색하였습니다.");
for( int childNode = 0; childNode < graph[nextNodes].length; childNode++ ) {
if( graph[nextNodes][childNode] != 0 && cache[childNode] == 0 ) {
nodesQue.add(childNode);
}
}
}
}
}
private void dfsLoopChecking( int orignalNode, int[] cache , Stack<Integer> nodesStack ) {
nodesStack.add( orignalNode );
while ( !nodesStack.isEmpty() ) {
Integer nextNodes = nodesStack.pop();
if( cache[nextNodes] == 0 ){
cache[nextNodes] = 1;
System.out.println( nextNodes + " 탐색하였습니다.");
for( int childNode = graph[nextNodes].length -1; childNode > 0; childNode-- ) {
if( graph[nextNodes][childNode] != 0 && cache[childNode] == 0 ) {
nodesStack.add(childNode);
}
}
}
}
}
}
GraphMatrix graph = new GraphMatrix(5);
graph.push(0, 1, 2);
graph.push(0, 2, 6);
graph.push(0, 4, 6);
graph.push(1, 2, 7);
graph.push(2, 4, 7);
graph.push(2, 3, 1);
graph.push(3, 4, 5);
graph.bfs(); // 0 1 2 4 3
graph.dfs(); // 0 1 2 3 4
참고자료
– 윤성우의 열혈 자료구조 ( C언어 )
– 위키백과
댓글남기기