JAVA 자료구조 1(Data Structure)
Step 1 : 자료구조(Data Structure)란 무엇인가?
자료 구조란 현실 세계 및 추상적 세계에서의 Data들의 모임 또 이런 Data들의 관계 등 Data들의 집합을 의미합니다. 신중히 선택한 자료구조 혹은 설계된 자료구조는 더 효율적인 알고리즘을 사용할 수 있게 하며 실행시간 및 메모리 용량과 같은 자원을 최소한으로 사용하면서 연산을 수행하도록 해줍니다. 자료구조는 원하는 형식으로 만들 수도 있으며, 지금부터 기존에 널리 알려진 자료구조 및 알고리즘을 풀면서 필요했던 다양한 자료구조에 대해 정리해 보겠습니다.
Step 2 : 단순구조
기본적으로 제공하는 자료형 및 추가로 정리한 자료형(BigDecimal)
정수
- byte, short, long, int, long
실수
- float, double
- BigDecimal
BigDecimal
실수형 소수점 사칙연산의 한계를 극복하며 큰 수를 다루기 위해 사용됩니다. 단점은 느립니다. BigDecimal number1 = new BigDecimal(“0.001”); BigDecimal number2 = new BigDecimal(“0.0007”);
더하기
number1 + number2 = number1.add(number2)
빼기
number1 - number2 = number1.subtract(number2)
곱하기
number1 * number2 = number1.multiply(number2)
나누기
number1.divide(number2, 3, RoundingMode.UP) // 올림
number1.divide(number2, 3, RoundingMode.HALF_UP) // 반올림
number1.divide(number2, 3, RoundingMode.DOWN) // 버림
나머지
number1.remainder(number2)
절대값
number1.abs()
최소값
number1.min(number2)
최대값
number1.max(number2)
논리적 비교
if( number1.compareTo(number2) == 1 ) {
System.out.println("number1 > number2");
} else if( number1.compareTo(number2) == 0 ) {
System.out.println("number1 == number2");
} else {
System.out.println("number1 < number2");
}
문자
- char
문자열
- String
Step 3 : 선형구조
리스트( List )
일반적으로 List형 자료구조는 배열과 같이 일자로 나열되어 서로 연결된 자료구조를 말합니다. 배열과의 차이점은 빈틈없이 자료를 적재하는 것이 목적인 자료구조입니다. 자료 중간의 삭제가 일어난다면 중간의 자료를 제거하고 앞뒤 연결이 필요합니다.
순차리스트
배열을 기반으로 구현된 리스트입니다. 장 : index로 바로 데이터를 가지고 올 수 있어 검색이 빠릅니다. 단 : 중간 데이터의 삭제가 일어난다면 삭제 후 다시 정리하는 과정이 필요하다는 것이 단점이기에 중간 데이터의 빈번한 수정이 일어난다면 추천하지 않습니다.
List<Integer> numberList= new ArrayList>();
연결리스트
데이터가 서로 연결된 형태의 자료형입니다. 장 : 데이터의 추가 삭제는 위치정보 수정만으로 가능하여 정보의 추가 삭제가 일어날 때 유용합니다. 단 : 검색을 위해서 자료를 순차적으로 확인해야 하기 때문에 검색에는 비효율 적입니다.
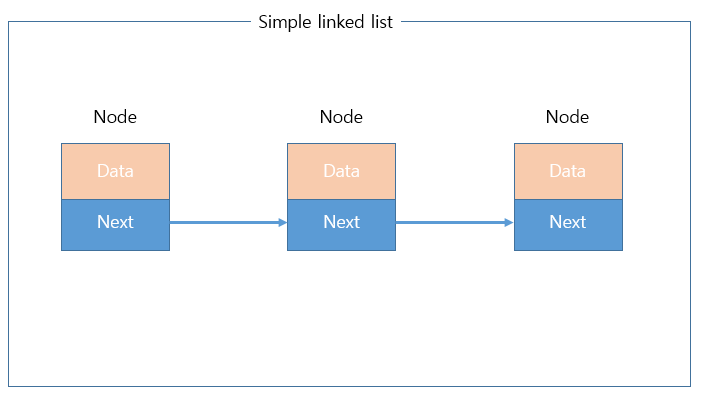
단순 연결 리스트 ( simple linked list )
가장 단순한 형태로 현재의 노드들은 다음 노드를 가리키는 하나의 참조 만을 가지고 있기에 한쪽 방향의 노드의 접근만 가능합니다.
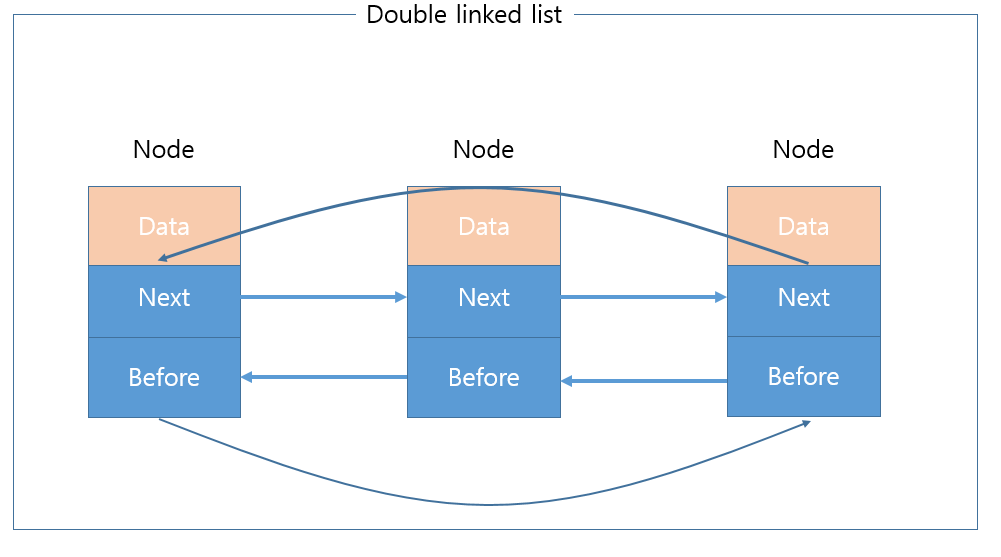
이중 연결 리스트( double linked list )
끝점과 시작점이 연결된 구조입니다.
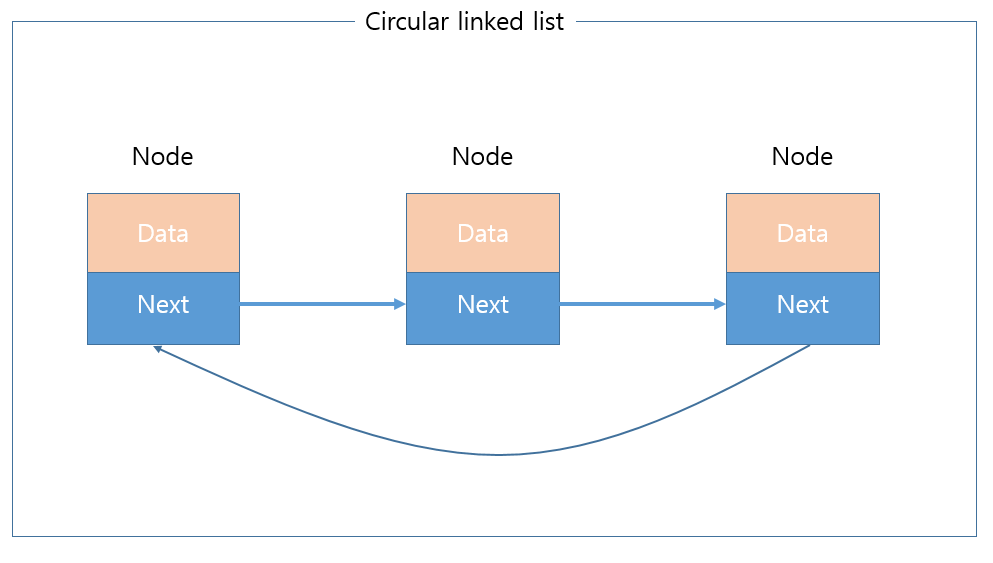
원형 연결 리스트 ( Circular linked list )
단순 연결 리스트 자료구조에서 마지막 노드를 첫 노드와 연결한 구조입니다.
위와 같은 개념적인 형상을 기반으로 원하는 형식으로 자료구조를 만들면 됩니다. 가볍게 이중 연결 리스트 자료구조를 만드는 방법을 보여드리겠습니다. java에서 제공하는 LinkedList 같은 경우 데이터를 저장하는 각 노드가 이전 노드와 다음 노드의 상태만 알고 있는 자료구조입니다. 이제 제일 복잡해 보이는 double linked list를 구현해 보겠습니다. 그리고 해당 자료구조를 만드는 데 필요한 add, remove 메서드, 그리고 특정 index 위치의 데이터를 추출하기 위한 get 메서드, 전체를 순회하는 toString메서드를 구현하겠습니다.
public class DoubleLinkedList<E> {
private Node<E> head;
private Node<E> tail;
private int size = 0;
public void add( E item ) {
Node<E> temp = new Node<>( item );
if( tail == null ) {
head = temp;
tail = temp;
} else {
Node<E> lastNode = getNode(size-1);
lastNode.next = temp;
temp.before = lastNode;
temp.next = head;
head.before = temp;
tail = temp;
}
System.out.println(temp.item +"이 삽입되어씁니다.");
size++;
}
private void checkingValidataion( int index ) {
if( size < index + 1 ) {
throw new IndexOutOfBoundsException("size를 확인하세요");
}
}
public void remove( int index ) {
Node<E> temp = getNode(index);
Node<E> nextNode = temp.next;
Node<E> beforeNode = temp.before;
beforeNode.next = nextNode;
nextNode.before = beforeNode;
System.out.println(temp.item +"이 지워졌습니다.");
if( index == 0 ) {
head = nextNode;
}
if( size == 1 ) {
head = null;
tail = null;
} else if( index == size-1 ) {
tail = beforeNode;
}
size--;
}
public E get( int index ) {
Node<E> temp = getNode(index);
return temp.item;
}
private Node<E> getNode( int index ) {
checkingValidataion(index);
Node<E> temp;
// 효율적 탐색을 위한 설계
if ( index < size / 2 ) {
// 앞에서 부터 찾기
temp = head;
for (int inner = 0; inner < index; inner++) {
temp = head.next;
}
} else {
//뒤에서 부터 찾기
temp = tail;
for (int inner = size - 1; inner > index; inner--) {
temp = temp.before;
}
}
return temp;
}
@Override
public String toString() {
if( size == 0 ) {
return "노드가 비었습니다.";
}
StringBuilder result = new StringBuilder();
Node<E> temp = head;
for( int index = 0; index < size; index++ ) {
result.append("노드 순회 index : ").append(index).append(" ").append(temp.item).append("\n");
temp = temp.next;
}
return result.toString();
}
// DoubleLinkedList에서 사용할 중첩클래스
private static class Node<E> {
E item;
Node<E> next;
Node<E> before;
public Node(E item ) {
this.item = item;
this.next = null;
this.before = null;
}
}
}
DoubleLinkedList<Integer> doubleLinked = new DoubleLinkedList<>();
doubleLinked.add(1);
doubleLinked.add(2);
doubleLinked.add(3);
doubleLinked.add(4);
System.out.println(doubleLinked.toString());
doubleLinked.remove(2);
System.out.println(doubleLinked.toString());
1
2
3
4
5
6
7
8
9
10
11
12
13
1이 삽입되어씁니다.
2이 삽입되어씁니다.
3이 삽입되어씁니다.
4이 삽입되어씁니다.
노드 순회 index : 0 1
노드 순회 index : 1 2
노드 순회 index : 2 3
노드 순회 index : 3 4
3이 지워졌습니다.
노드 순회 index : 0 1
노드 순회 index : 1 2
노드 순회 index : 2 4
스택(Stack)
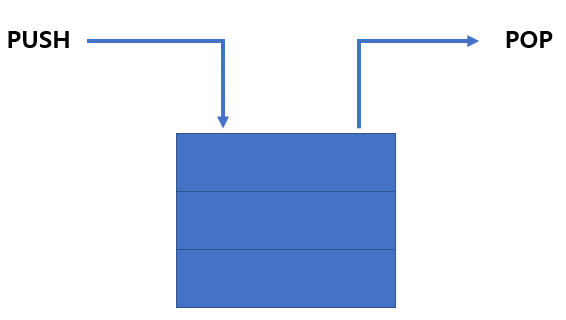
Stack이란 마지막에 들어온 데이터를 먼저 내보내는 후입선출(LIFO)을 표현하기 위한 자료구조입니다. 예를 들어 웹에서 History는 마지막 접근했던 페이지로 돌아가야 할 경우 이런 경우를 위해 사용하는 자료구조입니다. 위에서 작성했던 코드를 응용해서 push( 집어넣는 메서드 ), pop( 가져오는 메서드 ) 정도만 새로 작성한다면 기본적으로 사용할 수 있습니다.( 물론 push, pop 두 가지만으로는 불충분 합니다.) 필자는 자바에서 제공하는 java.util.Stack 라이브러리 stack을 사용하는 방법을 기술하겠습니다.
- push() : 마지막 위치에 데이터 삽입
- pop() : 마지막 데이터 제거 후 제거된 데이터 return
- peek() : 마지막에 들어온 데이터를 return 합니다.
- isEmpty() : stack이 비었는지 확인합니다.
Stack<String> stack = new Stack<>();
stack.push("first");
System.out.println("삽입 : " + stack.peek() );
stack.push("second");
System.out.println("삽입 : " + stack.peek() );
stack.push("third");
System.out.println( "삽입 : " + stack.peek() );
stack.push("forth");
System.out.println( "삽입 : " + stack.peek() );
for( String item : stack ){
System.out.println("순회 : " + item);
}
while( !stack.isEmpty() ) {
System.out.println("제거 : " + stack.pop() );
}
System.out.println("Stack이 비었습니까 : " + stack.isEmpty());
큐(Queue)
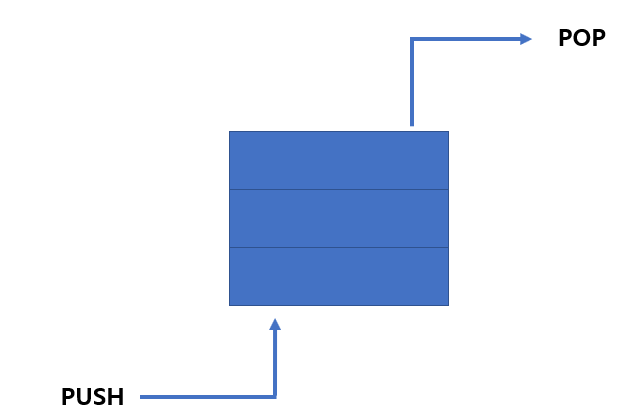
Queue란 먼저 들어온 데이터를 먼저 내보내는 선입선출(FIFO)을 표현하기 위한 자료구조입니다. 예를 들어 프린트나 테이블 예약 같은 경우 먼저 예약한 사람이 우선일 때 필요한 자료구조입니다.
java에서 que를 사용하기 위해서는 java.util.Queue를 구현한 클래스를 사용하면 됩니다. 내부 연결 구조를 배열로 만들었느냐, 연결 리스트 구조로 만들었느냐에 따라 내부 로직과 위 리스트에서 언급한 장단점이 생기게 되지만 사용법은 같습니다.
- add() : que자료구조에 데이터 삽입.
- peek() : 제일 먼저 들어와 상단에 위치한 데이터를 말합니다.
- poll() : 상단에 위치한 데이터를 추출하고 que에서 제거 합니다. 추출한 데이터를 return합니다.
- isEmpty() : stack이 비었는지 확인합니다.
Queue<String> queData = new ArrayDeque<String>();
// Queue<String> queData = new LinkedList<String>();
queData.add("first");
queData.add("second");
queData.add("third");
queData.add("forth");
for( String item : queData){
System.out.println("순회 : " + item);
}
while( ! queData.isEmpty() ) {
System.out.println("제거 : " + queData.poll() );
}
System.out.println("queData가 비었습니까 : " + queData.isEmpty());
우선순위 큐( Priority Queue )
선입 선출 구조의 Que와 다른 점은, 우선순위에 따라 우선순위가 높은 객체가 먼저 나오는 자료구조입니다. 우선순위 Que를 구현하는 방법은 배열 기반으로, 연결리스트를 기반으로, Heap을 이용하여 구현하는 방법이 존재합니다. 배열로 우선순위큐를 구현했을 경우 데이터 삽입, 삭제과정에서 데이터를 밀고 당기는 연산을 해야 하는 단점과 연결리스트로 우선순위 que를 구현하였을 경우 삽입의 위치를 찾기 위해 첫 번째 노드부터 마지막에 저장된 노드까지 순회해야 하는 기본적인 문제가 있어 더 좋은 성능을 발휘하는 Heap을 기반으로 구현하는 것이 일반적입니다. Heap은 tree 구조로 데이터를 정제하여 넣습니다. java.util.PriorityQueue을 사용한다는 것은 결국 heap을 구성하는 것이라고 봐도 무방합니다. 우선 Heap을 알기 전에 최종 목표인 Priority Queue의 사용법을 알아보겠습니다. 원론적으로 우선순위큐를 사용한다는 것은 Priority Queue에 들어갈 객체는 가중치가 다르다는 것이 기본이 됩니다. 그렇다면 Priority Queue에 들어갈 객체는 우선순위를 나타내기 위해 Comparable인터페이스의 compareTo 메서드를 구현하거나, 들어갈 객체를 변경할 수 없어 Comparable인터페이스를 구현하지 못하는 경우 Priority Queue생성 시 생성자로 Comparator인터페이스를 구현한 객체를 넘기면 됩니다. 두 방법 다 사용법을 확인해보겠습니다. 우선순위 큐에 넣을 객체는 Student로 시험 점수가 높은 사람을 top으로 위치하도록 우선순위 큐를 세팅하는 것입니다. 추가적인 욕심으로 동점자의 경우 사전식으로 정렬되도록 세팅하겠습니다. 아직 배우지 않았지만 java.util.PriorityQueue의 경우 기본 Heap구성은 minHeap으로 구성되기 때문에 상단에 위치한 데이터는 우선순위가 작은 값부터 위치한다고 보면됩니다. 당장 필요한 것은 우선순위가 높은 것이 위쪽에 위치하는 것이기 때문에 Comparator.reverseOrder()를 사용했다 정도만 이해하시면 되겠습니다. 그리고 우선순위가 높다는 것은 Comparator 혹은 compareTo 비교를 통해 +1 이 나오도록 하면 우선순위가 높다고 이해하시면 됩니다.
// Comparable 구현
public class Student implements Comparable<Student> {
private String name;
private int score;
public Student(String name, int score) {
this.name = name;
this.score = score;
}
@Override
public int compareTo(Student input) {
int result = Integer.compare(score, input.score);
if( result == 0 ) {
result = input.name.compareTo(name);
}
return result;
}
@Override
public String toString() {
return "이름 : " + name + " 점수 : " + score;
}
}
PriorityQueue<Student> priorityQueue = new PriorityQueue<>(Comparator.reverseOrder());
priorityQueue.add(new Student("김석진", 100));
priorityQueue.add(new Student("박석진", 90));
priorityQueue.add(new Student("진석진", 95));
priorityQueue.add(new Student("구석진", 88));
priorityQueue.add(new Student("다석진", 100));
priorityQueue.add(new Student("사석진", 100));
priorityQueue.add(new Student("나석진", 100));
1
2
3
4
5
6
7
8
// 출력
이름 : 김석진 점수 : 100
이름 : 나석진 점수 : 100
이름 : 다석진 점수 : 100
이름 : 사석진 점수 : 100
이름 : 진석진 점수 : 95
이름 : 박석진 점수 : 90
이름 : 구석진 점수 : 88
// comparator 이용
public class Student {
private String name;
private int score;
public Student(String name, int score) {
this.name = name;
this.score = score;
}
@Override
public String toString() {
return "이름 : " + name + " 점수 : " + score;
}
public String getName() {
return name;
}
public int getScore() {
return score;
}
}
PriorityQueue<Student> priorityQueue = new PriorityQueue<>( ( first, second )-> {
int result = Integer.compare(second.getScore(), first.getScore());
if( result == 0 ) {
result = first.getName().compareTo(second.getName());
}
return result;
}) ;
priorityQueue.add(new Student("김석진", 100));
priorityQueue.add(new Student("박석진", 90));
priorityQueue.add(new Student("진석진", 95));
priorityQueue.add(new Student("구석진", 88));
priorityQueue.add(new Student("다석진", 100));
priorityQueue.add(new Student("사석진", 100));
priorityQueue.add(new Student("나석진", 100));
while( !priorityQueue.isEmpty() ) {
Student student = priorityQueue.poll();
System.out.println(student.toString());
}
1
2
3
4
5
6
7
8
// 출력
이름 : 김석진 점수 : 100
이름 : 나석진 점수 : 100
이름 : 다석진 점수 : 100
이름 : 사석진 점수 : 100
이름 : 진석진 점수 : 95
이름 : 박석진 점수 : 90
이름 : 구석진 점수 : 88
Heap
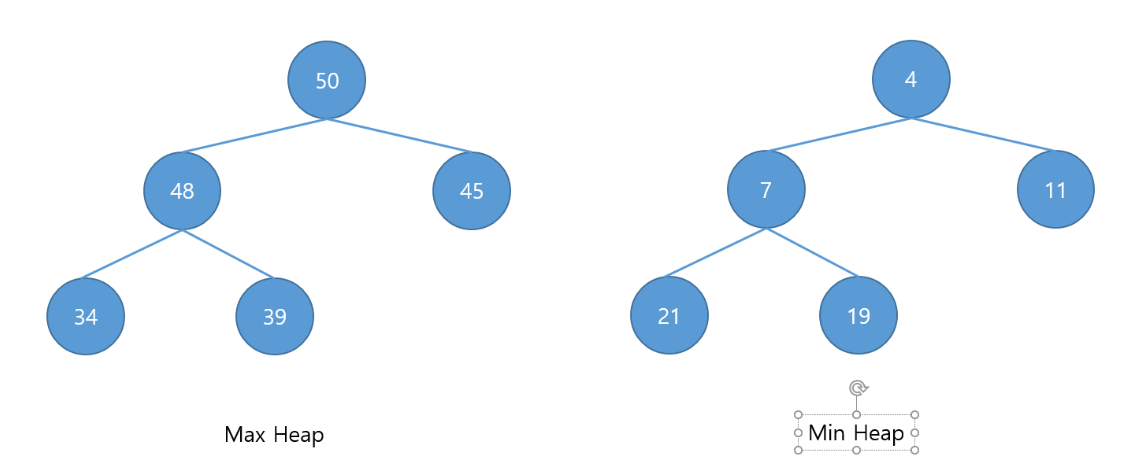 Heap이란 우선순위를 둔 우선순위 큐를 위해 필요한 자료구조로 부모의 노드는 항상 자식의 노드보다 클 경우를 Max heap, 작을 경우를 Min Heap라고 합니다. 그럼 Max Heap, Min Heap 자료구조를 구성하기 위해 직관적으로 필요한 데이터를 넣는 add, 맨 위 데이터를 뽑은 pop 메서드를 구현해보겠습니다. 또한, 위와 같은 tree구조를 표현하기 위해 Node가 아닌 배열을 통해 완전이진트리를 구성하겠습니다. 배열을 통해 Tree이진 트리 구성은 관련은 아래에서 더 자세하게 다루겠습니다. MaxHeap 구현 방법입니다.
Heap이란 우선순위를 둔 우선순위 큐를 위해 필요한 자료구조로 부모의 노드는 항상 자식의 노드보다 클 경우를 Max heap, 작을 경우를 Min Heap라고 합니다. 그럼 Max Heap, Min Heap 자료구조를 구성하기 위해 직관적으로 필요한 데이터를 넣는 add, 맨 위 데이터를 뽑은 pop 메서드를 구현해보겠습니다. 또한, 위와 같은 tree구조를 표현하기 위해 Node가 아닌 배열을 통해 완전이진트리를 구성하겠습니다. 배열을 통해 Tree이진 트리 구성은 관련은 아래에서 더 자세하게 다루겠습니다. MaxHeap 구현 방법입니다.
- add() : Max Heap의 경우 마지막 노드에 값을 넣은 후 부모 노드와 비교 후 들어온 값이 크면 부모 노드와 교체한다. 최 상위 꼭대기까지 같은 로직을 반복한다.
- pop() : Max Heap의 경우 꼭대기 값을 반환 후, 마지막 노드를 root 노드와 교체 후 자식 노드들과 크기 비교를 통해 자식이 클 경우 swap하는 로직을 통해 tree를 재구성 한다.
- isEmpty() : Heap이 비었는지 확인한다.
public class MaxHeap <T extends Comparable<T> > {
private int maxSize;
private int pointer; // 마지막 노드의 위치를 저장하기 위해 필요
private Object[] heap;
public MaxHeap( int arrSize ){
arrSize++;
maxSize = 1;
pointer = 0;
while( maxSize <= arrSize ) {
maxSize <<= 1;
}
this.heap = new Object[arrSize];
}
public void add( T item ) {
if(isFull()) {
throw new ArrayIndexOutOfBoundsException();
}
int tempIndex = ++pointer;
heap[pointer] = item;
while( tempIndex > 0 && tempIndex != 1) {
@SuppressWarnings("unchecked")
T parentValue = (T) heap[tempIndex/2];
if( parentValue.compareTo( item ) < 0) {
T swapData = parentValue;
heap[tempIndex/2] = item;
heap[tempIndex] = swapData;
} else {
break;
}
tempIndex /= 2;
}
}
@SuppressWarnings("unchecked")
public T pop() {
if(isEmpty()) {
throw new ArrayIndexOutOfBoundsException();
}
T result = (T)heap[1];
T lastChild = (T)heap[pointer];
heap[1] = lastChild;
heap[pointer--] = 0;
int tempIndex = 1;
while( tempIndex*2 <= pointer ) {
Boolean hasRightChild = tempIndex*2+1 <= pointer;
T leftChild = (T)heap[tempIndex*2];
T rightChild = (T)heap[tempIndex*2+1];
T parent = (T)heap[tempIndex];
T changeValue = null;
int changeIndex;
if( !hasRightChild ) {
if( parent.compareTo(leftChild) > 0 ) break;
changeIndex = tempIndex*2;
changeValue = leftChild;
} else {
if( parent.compareTo(leftChild) > 0 && parent.compareTo(rightChild) > 0 ) break;
changeValue = leftChild.compareTo(rightChild) < 0? rightChild : leftChild;
changeIndex = leftChild.compareTo(rightChild) < 0? tempIndex*2+1 : tempIndex*2;
}
//교체
heap[tempIndex] = changeValue;
heap[changeIndex] = parent;
tempIndex = changeIndex;
}
return result;
}
public boolean isEmpty() {
return pointer == 0;
}
private boolean isFull() {
return pointer >= maxSize;
}
}
MaxHeap<Student> maxHeap = new MaxHeap<>(7);
maxHeap.add(new Student("김석진", 100));
maxHeap.add(new Student("박석진", 90));
maxHeap.add(new Student("진석진", 95));
maxHeap.add(new Student("구석진", 88));
maxHeap.add(new Student("다석진", 100));
maxHeap.add(new Student("사석진", 100));
maxHeap.add(new Student("나석진", 100));
1
2
3
4
5
6
7
8
//출력
이름 : 김석진 점수 : 100
이름 : 나석진 점수 : 100
이름 : 다석진 점수 : 100
이름 : 사석진 점수 : 100
이름 : 진석진 점수 : 95
이름 : 박석진 점수 : 90
이름 : 구석진 점수 : 88
덱( Deque )
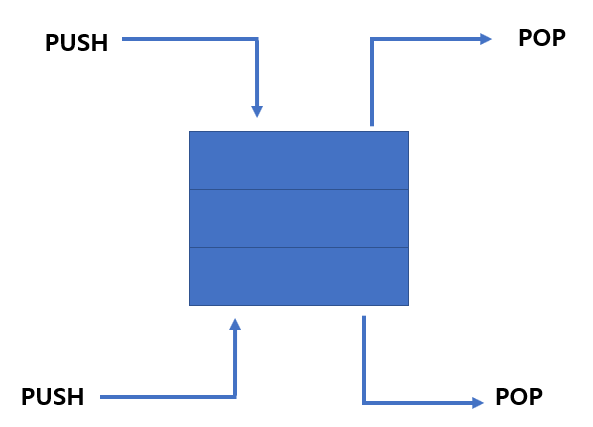 Deque란 Stack과 queue 양쪽으로 엘리먼트의 삽입과 삭제를 수행할 수 있는 자료구조 입니다.
Deque란 Stack과 queue 양쪽으로 엘리먼트의 삽입과 삭제를 수행할 수 있는 자료구조 입니다.
- add() : 데이터를 que형식으로 삽입합니다..
- addFirst() : 데이터를 위에서 삽입합니다.(Stack 형식)
-
addLast() : 데이터를 아래에서 삽입합니다.(Que 형식 == add() )
- poll() : que의 poll과 같은 기능을 합니다.
- pollFirst() : que의 poll과 같은 기능을 합니다.
- pollLast() : deque의 하단에 tail 쪽의 데이터를 제거하고 return합니다.
//Deque<String> deque = new LinkedList<>();
Deque<String> deque = new ArrayDeque<String>();
deque.addLast("first");
deque.addLast("second");
deque.addLast("third");
deque.addLast("forth");
for( String item : deque ){
System.out.println("순회 : " + item);
}
while( !deque.isEmpty() ) {
System.out.println("제거 : " + deque.pollLast() );
}
System.out.println("Stack이 비었습니까 : " + deque.isEmpty());
참고자료
– 윤성우의 열혈 자료구조 ( C언어 )
– 위키백과

댓글남기기