JAVA 알고리즘 2 (Algorithm)
분할 정복 ( Divide & Conquer )
분할 정복 알고리즘은 유명한 알고리즘 패턴으로 각개 격파라는 표현을 사용할 수 있습니다. 주어진 문제를 둘 이상의 부분 문제로 나눈 뒤 각 문제에 대한 답을 재귀 호출로 이용해 계산하고, 각 부분의 답으로부터 전체의 해답을 계산하는 방법입니다. 분할 정복 알고리즘들은 대개 세 가지의 구성 요소를 가지고 있습니다.
- 문제를 더 작은 문제로 분할하는 과정 ( divide )
- 각 문제에 대한 답을 원래 문제에 대한 답으로 병합하는 과정 ( merge )
- 더는 답을 분할하지 않고 곧장 풀 수 있는 매우 작은 문제 ( base case )
분할 정복을 위해서는 몇 가지 특정이 성립해야 합니다. 우선 문제를 둘 이상의 부분 문제로 나누는 자연스러운 방법이 있어야 하고, 부분 문제의 답을 조합해 원래 문제의 답을 계산하는 효율적인 방법이 있어야 합니다.
fastSum(n) = 1+2+3+4+…+n
완전 탐색을 통한 단순 for문으로 해결할 수 있지만, 조금 더 효율적인 알고리즘을 짜보겠습니다.
Divice, Merge : (1+2+3+..+n/2) + ((n/2+1) +(n/2+2)+…+n)
해당 형식으로 분할 한다면 앞쪽은 fastSum(2/n)으로 표시 가능합니다. 두 번째 부분은 a부터 b까지의 합으로 표현되므로 이를 fastSum형식으로 나타 낼 수 있어야 분할이 가능합니다. 해당은 ((n/2+1) +(n/2+2)+…+n) = ((n/2+1) +(n/2+2)+…+(n/2 +n/2) 로 나타낼 수 있기 때문에 결국 n/2 * n/2 + (1+2+3+..+n/2) 으로 가능하기 때문에 최종적으로는 fastSum(n) = fastSum(2/n) + n/2 * n/2 + fastSum(2/n) = 2 X fastSum(2/n) + n^2/4 로 표현 가능합니다. 단 이는 짝수일 때만 가능하기 때문에 홀수 일 때도 따로 처리가 필요합니다.
Base Case : n이 1일때는 따로 계산이 필요없습니다.
private static int fastSum(int n) {
if( n == 1 ) {
return 1;
} else if(n % 2 == 1) {
return fastSum(n-1) + n;
} else {
return 2*fastSum(n/2) + (n*n)/4;
}
}
쿼드 트리 뒤집기
대량의 좌표데이터를 메모리 안에 압축해 저장하기 위해 사용하는 기술 중 Quad Tree란 것이 있습니다. 대표적으로 흑백 그림을 압축해 표현하는 것입니다. 2^n * 2^n 크기의 흑백 그림을 다음과 같은 과정을 거쳐 문자열로 압축하는 것입니다.
- 그림이 모두 검은색일 경우 압축 결과는 그림 크기와 관계없이 b입니다.
- 그림이 모두 흰색일 경우 압축 결과는 그림 크기와 관계없이 w입니다.
- 픽셀이 같은 색이 아니라면 쿼드 트리는 이 그림을 가로세로 각각 2등분해 4개의 조각으로 쪼갠 뒤 각각을 쿼드 트리 압축합니다. 이때 전체 그림의 압축 결과는 x(왼쪽 위 압축결과)(오른쪽위 압축 결과)(왼쪽 아래 압축결과)(오른쪽 아래 압축결과)
- 만약 전체 그림의 압축 결과가 xxwww bxwxw bbbww xxxww bbww wwbb가 주어졌을 때 이 그림을 상하로 뒤집은 그림을 쿼드 트리 압축해서 출력하는 프로그램을 작성하시오.
가장 무식한 방법은 그림을 다시 원래대로 만들고, 상하 반전, 쿼드트리압축 과정을 수행하는 것입니다. 다만 입력이 특정 이상이 될 경우 해당 방법은 사용할 수 없습니다. 이에 우리는 두 가지의 접근 방법을 생각해야 합니다.
- 큰 입력에도 동작하는 효율적인 알고리즘을 처음부터 새로 만들기
- 작은 입력에 대해서만 동작하는 알고리즘으로부터 시작해 최적화해 나가기.
둘 중 어느 접근이 맞는지 판단하기는 쉽지 않습니다. 하지만 접근하기 쉬운 방법은 두 번째 방법으로 단순한 알고리즘으로 시작해 최적화해 가는 것입니다.
우선 가장 중요한 쿼드트리의 압축을 어떻게 풀어나가야 하는지 알아보겠습니다.
쿼드트리 자체가 재귀적으로 구성되어 있기 때문에 트리를 압축하거나 해제하는 과정 또한 재귀 호출로 정의하는 것이 자연스럽습니다.
압축을 해제하여 n * n의 이미지로 복구하는 decompress() 함수입니다. ( n은 주어졌다고 가정해야 해제할 수 있습니다. 예제는 16 * 16 이미지를 복구하는 것으로 하겠습니다. )
private static int inputIndex = 0;
public static void main(String args[]){
quardTreeDraw("xxwwwbxwxwbbbwwxxxwwbbbwwwwbb", 16);
}
private static void quardTreeDraw( String input , int n) {
String[][] xy = new String[n][n];
decompress(0, 0, n, input, xy );
String result = "";
for( int yindex = 0; yindex < n; yindex++ ) {
for( int xIndex = 0; xIndex< n; xIndex++ ) {
result += xy[yindex][xIndex] + " ";
}
result +="\n";
}
System.out.println(result);
}
private static void decompress( int x, int y, int n, String input, String[][] xy) {
char inputItem = input.charAt(inputIndex++);
if( inputItem == 'w' ) {
for( int yIndex = 0; yIndex < n; yIndex++ ) {
for( int xIndex = 0; xIndex < n; xIndex++ ) {
xy[y + yIndex][ x + xIndex] = "-";
}
}
} else if( inputItem == 'b' ) {
for( int yIndex = 0; yIndex < n; yIndex++ ) {
for( int xIndex = 0; xIndex < n; xIndex++ ) {
xy[y + yIndex][ x + xIndex] = "+";
}
}
} else {
int half = n/2;
decompress( x, y, half, input, xy );// 좌상.
decompress( x+half, y, half, input, xy );// 우상.
decompress( x, y+half, half, input, xy );// 좌하.
decompress( x+half, y+half, half, input, xy );// 우하.
}
}
이제 근본적으로 문제를 풀어봅시다. 재귀를 이용하는 것은 확실하며, 단순히 원하는 것은 뒤집은 그림입니다. ‘뒤집다’의 개념은 위아래가 바뀌는 것입니다. 즉 4등분으로 나누었을 때, 상하가 바뀌는 것이며, w, b일 때는 뒤집지 뒤집을 필요가 없어서 그대로를 return 하는 것입니다. 즉 작은 문제로 분할 ( 4등분 한다. ) , 병합과정, base case를 코드로 표현하면 아래와 같습니다.
private static int inputIndex = 0;
public static void main(String args[]){
quardTreeRevers("xxwwwbxwxwbbbwwxxxwwbbbwwwwbb", 16);
}
private static void quardTreeRevers( String input , int n) {
String result = revers( input );
System.out.println(result);
}
private static String revers( String input ) {
char inputItem = input.charAt(inputIndex++);
if( inputItem == 'w' || inputItem == 'b' ) {
return String.valueOf(inputItem);
} else {
String leftUp = revers(input);
String rightUp = revers(input);
String leftDown = revers(input);
String rightDown = revers(input);
return "x" + leftDown + rightDown + leftUp + rightUp;
}
}
울타리 잘라내기
너비가 같은 일정한 울타리가 있습니다. 시간이 지남에 따라 판자들이 부서지거나 망가져 높이가 불규칙적으로 변한 관계로 울타리를 통째로 교체하기로 했습니다. 이 때, 버리는 울타리의 일부를 직사각형으로 잘라 재활용 하고 싶습니다. 만약 input으로 fence의 높이가 배열로 주어질 때, 최대로 재활용 할 수 있는 fence의 크기를 계산하는 알고리즘을 도출하시오. 단 아래 이미지의 3번째 처럼 대각선은 불가능 합니다. ( input의 최대 크기는 20000개 )
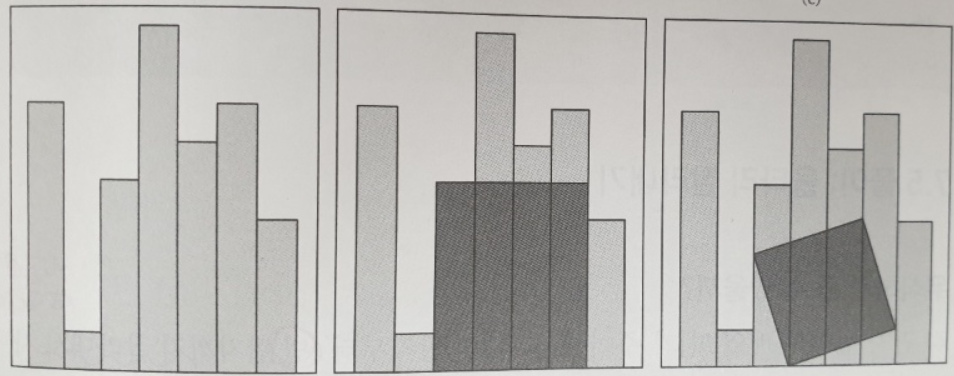
완전탐색
만약 완전 탐색으로 문제를 푼다면, 기둥 하나를 처음부터 끝가지 잘라서 매치 해보는 것입니다.
private static int maxIndex = 0;
public static void main(String args[]){
int[] input = {1,4,4,4,4,1,1}; // 결과 16
System.out.println(maxFence(input));
}
private static int maxFence(int[] input) {
int result = 0;
maxIndex = input.length;
for( int left = 0; left < maxIndex; left++ ) {
int minHeight = input[left];
for( int right = left; right < maxIndex; right++ ) {
minHeight = Math.min(minHeight, input[right]);
result = Math.max(result, minHeight*(right - left +1 ));
}
}
return result;
}
해당 방법은 2중 for문으로 인해 input의 최대 크기가 20000개 이기 때문에 20000*20000 4억번의 연산이 필요해 통과하기 어려울 수 있습니다.
분할정복
만약 이 문제를 분할정복으로 푼다면 어떻게 풀 수 있을까요? 최대 넓이를 찾는다를 기준으로 중간을 기점으로 왼쪽 영역의 최대, 오른쪽 영역의 최대로 나누어 회귀를 적용한다면 속도가 어마하게 빨라질 것 같습니다. 단. 걸쳐있을 때도 가정해야 합니다. 걸쳐있을 때는 걸쳐있는 모든 경우의 max를 비교하여 찾으면 됩니다. 아래 이미지 처럼 2개로 시작하여, 왼쪽 오른쪽을 비교하여 더 큰 막대기쪽으로 작은것 기준으로 넓혀가면서 면적을 비교하는 것입니다.
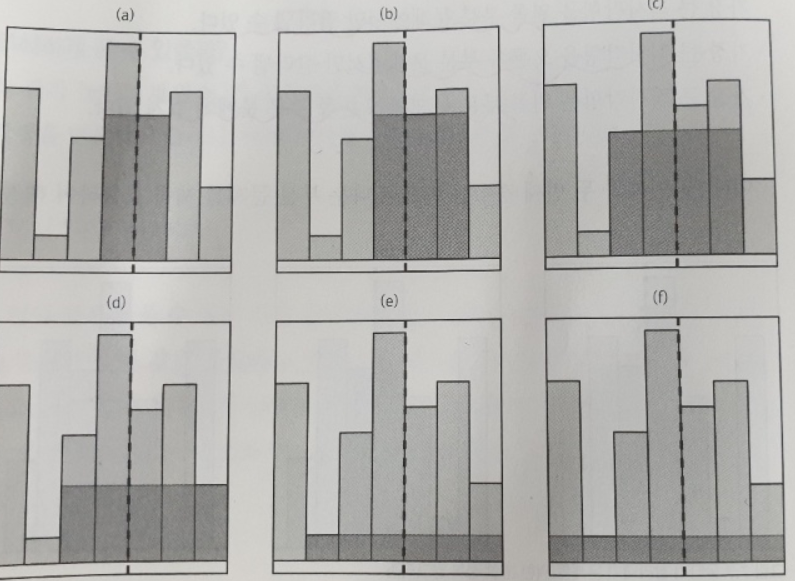
private static int maxIndex = 0;
private static int[] inputData;
public static void main(String args[]){
int[] input = {1,4,4,4,4,1,1}; // 결과 16
System.out.println(maxFence(input));
}
private static int maxFence(int[] input) {
inputData = input;
maxIndex = input.length-1;
return solve( 0, maxIndex );
}
private static int solve( int start, int end ) {
if( start == end ) {
return inputData[start];
} else {
int mid = ( start + end )/2;
int leftMax = solve( start, mid );
int rightMax = solve( mid+1, end );
int result = Math.max(leftMax, rightMax);
int leftCheck = mid;
int rightCheck = mid+1;
int height = Math.min(inputData[leftCheck], inputData[rightCheck]);
result = Math.max(result, height*2); // 중앙에 걸쳐있는 2개가 최대인 경우 확인.
while( start < leftCheck || rightCheck < end ) {
if( rightCheck < end && ( leftCheck == start || inputData[leftCheck-1] < inputData[rightCheck+1] ) ) {
rightCheck++;
height = Math.min(height, inputData[rightCheck]);
// 우측으로 확장해야하는 케이스 외 모두 좌측 확장
// 왼쪽이 끝났거나, 왼쪽보다 오른쪽 막대가 더 커서 우측으로 자를 수 있을 때.
} else {
leftCheck--;
height = Math.min(height, inputData[leftCheck]);
}
result = Math.max(result, (rightCheck-leftCheck+1)*height); // 좌 우 확장해 나가면서 확인
}
return result;
}
}
해당 방법은 중간에 1/2씩 나누어 집니다. 결국 O(logN)과 내부적으로 중간 확인을 위한 N번씩 반복이 존재함으로 O(NlogN) 즉 대략 29만번의 연산이면 해답을 구할 수 있어 시간내에 충분히 풀 수 있습니다.
참고자료
– 인사이트 - 프로그래밍대회에서 배우는 알고리즘 문제해결 전략( 저자 - 구종만 ) ( C언어 )

댓글남기기